Section 7.2 Polar Form
Preview Activity 7.2.1.
The code in 7.2.1 plots the complex numbers \((1+i)^0,(1+i)^1,(1+i)^2,(1+i)^3\text{,}\) along with a line connecting to each number from the origin.
complex_number = CDF(1,1)
graph = points(
[CDF(complex_number^power) for power in range(4)],
xmin=-10,ymin=-10,xmax=10,ymax=10,
aspect_ratio=1,
pointsize=30
)
for power in range(4):
graph+=line([CDF(0),CDF(complex_number^power)])
graph
(a)
Run 7.2.1. Then copy this code into three other code cells, modifying complex_number to be \(2i\text{,}\) \(\sqrt{3}-i\text{,}\) and \(-0.7+1.8i\text{.}\)
(b)
What do you notice? (Write a sentence.)
(c)
What do you wonder? (Write a sentence.)
Activity 7.2.2.
One important property for a complex number is its modulus or absolute value, which measures the distance between that number and the origin \(0+0i\text{.}\) For example, the modulus \(|4-3i|\) of \(4-3i\) happens to be \(5\text{,}\) illustrated in 7.2.2.
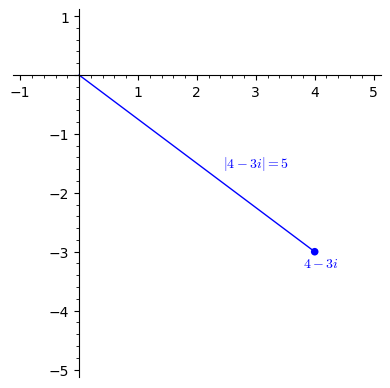
(a)
Plot each of the following complex numbers in the plane. Then describe the modulus for each number.
\(\displaystyle 3\)
\(\displaystyle 2i\)
\(\displaystyle -4i\)
\(\displaystyle -1\)
(b)
SageMath confirms that the modulus of \(4-3i\) is \(5\) by running the following code: abs(CDF(4,-3)).
Use Code cells to confirm your modulus calculations from the previous task.
(c)
Modify 7.2.1 to plot the following complex numbers. Then calculate their moduli using technology, to confirm that the largest modulus belongs to the number furthest from the origin, and the smallest modulus belongs to the number closest to the origin.
\(\displaystyle 12+5i\)
\(\displaystyle -6+8i\)
\(\displaystyle \sqrt{3}-i\)
\(\displaystyle -3-3i\)
(d)
The formula to compute the modulus of \(a+bi\) is
Calculate the four moduli from the previous task using this formula.
(e)
The Pythagorean Theorem says that \(a^2+b^2=c^2\text{,}\) where \(a,b\) are the leg lengths of a right triangle, and c is the length of its hypotenuse, illustrated in 7.2.3.
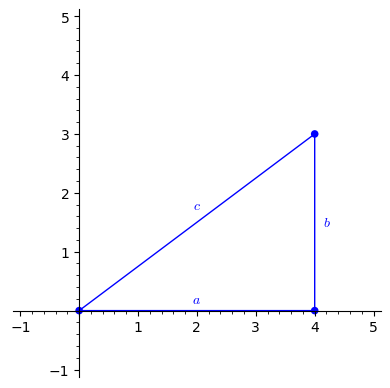
Write a sentence or two explaining why this theorem is related to the formula for the modulus of a complex number.
Activity 7.2.3.
Another important property of complex numbers is their argument. An argument of \(0\) means that the complex number is on the right half of the horizontal axis, a positive argument means that the complex number is rotated counter-clockwise above the horizontal axis, and a negative argument means that the complex number is rotated clockwise below the horizontal axis.
SageMath can calculate the argument of a complex numbers as follows: arg(CDF(4,-3)), returning approximately \(-0.6435\text{.}\) (We often use approximations because arguments are usually irrational numbers; why this is so requires trigonometry, so we leave that for another day.)
(a)
Use SageMath to find the arguments for each of the following numbers you plotted earlier.
\(\displaystyle 12+5i\)
\(\displaystyle -6+8i\)
\(\displaystyle \sqrt{3}-i\)
\(\displaystyle -3-3i\)
(b)
Make up several other complex numbers and find their arguments. What values does it seem that an argument is allowed to have? Do you notice anything special or familiar about this range?
Activity 7.2.4.
Complex numbers are often written in polar form, where \(r\) describes the modulus and \(\theta\) describes the argument:
For example, the polar form of \(4-3i\) is (approximately) \(5\exp(-0.6435i)\text{,}\) which may be confirmed by running 5*exp(-0.6435*CDF(I)) in a Code cell.
(a)
Write each of the following complex numbers in their polar forms, using their moduli and an approximation of their arguments found earlier:
\(\displaystyle 12+5i\)
\(\displaystyle -6+8i\)
\(\displaystyle \sqrt{3}-i\)
\(\displaystyle -3-3i\)
(b)
Use SageMath to confirm each of the (approximate) polar forms you found in the previous task.
Activity 7.2.5.
Adding complex numbers combines their horizontal and vertical components. Multiplying a complex number by a real number scales its distance from the origin. But what does it mean to multiply two complex numbers?
(a)
Describe the modulus, argument, and polar form for each complex number:
\(\displaystyle \frac{9}{5}+\frac{12}{5}i\)
\(\displaystyle \frac{24}{13}+\frac{10}{13}i\)
\((\frac{9}{5}+\frac{12}{5}i)\cdot(\frac{24}{13}+\frac{10}{13}i)\) (use SageMath to multiply these)
(b)
Compare the moduli of the product with the moduli of each factor. What relationship do you notice?
(c)
Compare the argument of the product with the arguments of each factor. What relationship do you notice?
(d)
Write a few sentences conjecturing what you think multiplying complex numbers does with their moduli and arguments. Then make up several examples to try and support your conjecture.
Activity 7.2.6.
Use a Code cell to confirm \(i\cdot i=-1\text{,}\) that is, \(i^2=-1\text{.}\) Then write a few sentences defending this result using what you've discovered about how multiplication affects moduli and arguments.
Exercises Exercises
1.
Write a sentence describing why the modulus of \(-5i\) is \(5\text{.}\)
2.
Show how to find the modulus of \(-6+8i\) using both SageMath and a formula.
3.
Find the arguments for \(3+2i\) and \(3-2i\text{.}\) Then write a sentence explaining why these arguments are negatives of each other.
4.
Find the polar form of \((2-i)\cdot(1+3i)\) by using the moduli and arguments of \(2-i\) and \(1+3i\text{.}\)
5.
Use SageMath to compute \((2-i)\cdot(1+3i)\) from its polar form found in the previous exercise.
6.
Use SageMath to multiply \((2-i)\cdot(1+3i)\) directly.