Section 7.1 Cartesian Coordinates
Preview Activity 7.1.1.
To describe points in a two-dimensional Cartesian plane, we may use either ordered pairs \((x,y)\) or complex numbers \(x+yi\text{.}\) These are simply two different ways to describe the same positional data. For example, both \((-1,5)\) and \(-1+5i\) describe the same point in the illustration found in 7.1.1.
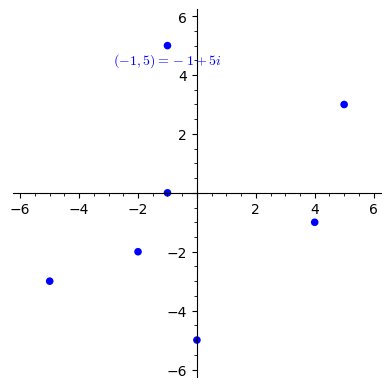
The origin is the point \((0,0)=0+0i\) at the “center” of the plane. The \(x\)-value of any point (the first number in the pair, and the value without an \(i\) in the complex number) describes its horizontal distance from the origin, moving right for positive numbers, and left for negative numbers. Likewise the \(y\)-value of any point (the second number in the pair, and the value with an \(i\) in the complex number) describes its vertical distance from the origin, where positive is up and negative is down.
(a)
Draw 7.1.1 by hand, or copy it into a graphics program. Then label the following points with both ordered pairs and complex numbers.
\(\displaystyle (-5,-3)\)
\(\displaystyle 5+3i\)
\(\displaystyle 4-1i\)
(b)
Note that \(4-1i\) is often written as \(4-i\text{,}\) since we think of \(1i\) as multiplication. How might \(0-5i\) be more simply written? What about \(-1+0i\text{?}\)
(c)
Label \(0-5i\) and \(-1+0i\) in your drawing with both ordered pairs and simplified complex numbers.
Activity 7.1.2.
Both ordered pairs \((x,y)\) and complex numbers \(x+yi\) can be used to describe points in the plane. Ordered pairs are a kind of vector, which we'll discuss in the next chapter. For now, let's explore how SageMath can be used to handle complex numbers.
(a)
In SageMath, there are a few ways to describe complex numbers. We will use the symbol CDF() tool along with the arithmetic operators +,-,*,/. For example, \(4-5i\) can be displayed by a Code cell by running show(4-5*CDF(I)).
Display the complex number \(-5+2i\) using a Code cell. (Note that by default, SageMath will use decimal expressions for whole values in a complex number; that's okay.)
(b)
A useful shortcut is to assign i=CDF(I). Then show(4-5*CDF(I)) can be shortened to show(4-5*i). (Pay attention to capitalization, though!)
Use this shortcut to display \(3+4i\) from a Code cell.
(c)
Another shortcut to work with complex numbers in SageMath is to describe the equivalent ordered pair: show(CDF(4,-5)) again produces \(4-5i\text{.}\)
Use this shortcut to display \(-6-i\) from a code cell.
(d)
Run show(3*i-5-7*i+3) and show(4*(i-2)) in a Code cell. Then write a couple sentences explaining how you think these results were obtained.
(e)
Show how to compute \(7+4i-6i-5\) and \(3(2-3i)\) by hand. Then confirm your results using Code cells.
Activity 7.1.3.
SageMath provides the points() tool to plot points in the Cartesian plane, demonstrated in 7.1.2.
# Example list of complex numbers
complex_list = [3, 4-2*CDF(I), CDF(-1,5)]
# Plot complex_list in the plane
points(
[CDF(x) for x in complex_list],
xmin=-6,ymin=-6,xmax=6,ymax=6,
aspect_ratio=1,
pointsize=30
)
(a)
Modify and run 7.1.2 in a Code cell to plot the following complex numbers.
\(\displaystyle 3-5i\)
\(\displaystyle 4i\)
\(\displaystyle -2\)
\(\displaystyle -4+3i\)
(b)
Write a sentence explaining where you'd expect the numbers \(-5i+3\) and \(3i-4\) to be located in the plane. Then use technology to confirm your intuition. (If you were mistaken, add a sentence explaining why you think they ended up where they did instead.)
(c)
Modify and run 7.1.2 in a Code cell to plot the following complex numbers. (You'll need to figure out how to resize the visible portion of the plane.)
\(\displaystyle 10+i\)
\(\displaystyle 9\)
\(\displaystyle -4+8i\)
Activity 7.1.4.
The usefulness of complex numbers comes from their ability to describe movement of points in the plane.
(a)
Use a Code cell to plot the following complex numbers:
The origin, that is, \(0+0i\)
\(\displaystyle -2+3i\)
\(\displaystyle 4-i\)
The complex number that is two units left and three units up from \(4-i\text{.}\)
\(\displaystyle (4-i)+(-2+3i)\)
(b)
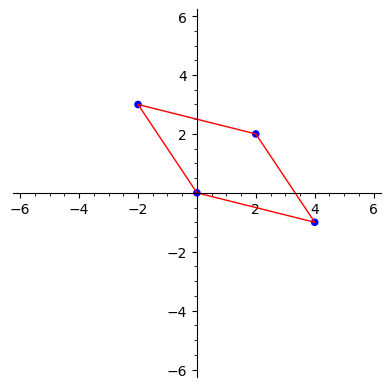
Write a sentence or two explaining what the illustration in 7.1.3 says about your plot in the previous task.
(c)
Use a Code cell to show the following complex numbers in a new plot.
\(\displaystyle 0+0i\)
\(\displaystyle 1+4i\)
\(\displaystyle 2-i\)
\(\displaystyle (1+4i)+(2-i)\)
\(\displaystyle 3+3i\)
(d)
Write a sentence or two describing the “purpose” for adding a pair of complex numbers like \((1+4i)+(2-i)\text{.}\)
(e)
Use a Code cell to show the following complex numbers in a new plot.
\(\displaystyle 2+3i\)
\(\displaystyle 2(2+3i)\)
(f)
Use a Code cell to show the following complex numbers in a new plot.
\(\displaystyle -1+2i\)
\(\displaystyle 3(-1+2i)\)
(g)
Write a sentence or two describing the “purpose” for multiplying a complex number by a real number like \(2(2+3i)\) or \(3(-1+2i)\text{.}\)
Exercises Exercises
1.
Illustrate how to plot the position of the complex number \(3-4i\) in the plane by hand. Label it with its complex number and the equivalent ordered pair.
2.
Use a Code cell to plot all of the following complex numbers in the plane.
\(\displaystyle 3+i\)
\(\displaystyle -5\)
\(\displaystyle -2+4i\)
\(\displaystyle 2i\)
\(\displaystyle -3-5i\)
\(\displaystyle 1-i\)
3.
Write a sentence explaining where the complex number \((3+2i)+(-4+i)\) is positioned when compared to \(3+2i\text{.}\) Then illustrate your sentence by hand or using technology.
4.
Show how to calculuate the value of \((3+2i)+(-4+i)\) by hand and using technology.
5.
Write a sentence explaining where the complex number \(2(1-3i)\) is positioned when compared to \(1-3i\text{.}\) Then illustrate your sentence by hand or using technology.
6.
Show how to calculuate the value of \(2(1-3i)\) by hand and using technology.